The Scientific Dogma

Modern science has no dogma. Yet it has a common core of research methods, which are all based on collecting empirical observations – those we can observe with at least one of our senses – and putting them together with the help of mathematical tools.

People throughout history collected empirical observations, but the importance of these observations was usually limited. Why waste precious resources obtaining new observations when we already have all the answers we need? But as modern people came to admit that they did not know the answers to some very important questions, they found it necessary to look for completely new knowledge. Consequently, the dominant modern research method takes for granted the insufficiency of old knowledge. Instead of studying old traditions, emphasis is now placed on new observations and experiments. When present observation collides with past tradition, we give precedence to the observation. Of course, physicists analysing the spectra of distant galaxies, archaeologists analysing the finds from a Bronze Age city, and political scientists studying the emergence of capitalism do not disregard tradition. They start by studying what the wise people of the past have said and written. But from their first year in college, aspiring physicists, archaeologists and political scientists are taught that it is their mission to go beyond what Einstein, Heinrich Schliemann and Max Weber ever knew.

Mere observations, however, are not knowledge. In order to understand the universe, we need to connect observations into comprehensive theories. Earlier traditions usually formulated their theories in terms of stories. Modern science uses mathematics.

There are very few equations, graphs and calculations in the Bible, the Qur’an, the Vedas or the Confucian classics. When traditional mythologies and scriptures laid down general laws, these were presented in narrative rather than mathematical form. Thus a fundamental principle of Manichaean religion asserted that the world is a battleground between good and evil. An evil force created matter, while a good force created spirit. Humans are caught between these two forces, and should choose good over evil. Yet the prophet Mani made no attempt to offer a mathematical formula that could be used to predict human choices by quantifying the respective strength of these two forces. He never calculated that ‘the force acting on a man is equal to the acceleration of his spirit divided by the mass of his body’.

This is exactly what scientists seek to accomplish. In 1687, Isaac Newton published The Mathematical Principles of Natural Philosophy, arguably the most important book in modern history. Newton presented a general theory of movement and change. The greatness of Newton’s theory was its ability to explain and predict the movements of all bodies in the universe, from falling apples to shooting stars, using three very simple mathematical laws:

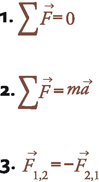
Henceforth, anyone who wished to understand and predict the movement of a cannonball or a planet simply had to make measurements of the object’s mass, direction and acceleration, and the forces acting on it. By inserting these numbers into Newton’s equations, the future position of the object could be predicted. It worked like magic. Only around the end of the nineteenth century did scientists come across a few observations that did not fit well with Newton’s laws, and these led to the next revolutions in physics – the theory of relativity and quantum mechanics.

Newton showed that the book of nature is written in the language of mathematics. Some chapters (for example) boil down to a clear-cut equation; but scholars who attempted to reduce biology, economics and psychology to neat Newtonian equations have discovered that these fields have a level of complexity that makes such an aspiration futile. This did not mean, however, that they gave up on mathematics. A new branch of mathematics was developed over the last 200 years to deal with the more complex aspects of reality: statistics.

In 1744, two Presbyterian clergymen in Scotland, Alexander Webster and Robert Wallace, decided to set up a life-insurance fund that would provide pensions for the widows and orphans of dead clergymen. They proposed that each of their church’s ministers would pay a small portion of his income into the fund, which would invest the money. If a minister died, his widow would receive dividends on the fund’s profits. This would allow her to live comfortably for the rest of her life. But to determine how much the ministers had to pay in so that the fund would have enough money to live up to its obligations, Webster and Wallace had to be able to predict how many ministers would die each year, how many widows and orphans they would leave behind, and by how many years the widows would outlive their husbands.

Take note of what the two churchmen did not do. They did not pray to God to reveal the answer. Nor did they search for an answer in the Holy Scriptures or among the works of ancient theologians. Nor did they enter into an abstract philosophical disputation. Being Scots, they were practical types. So they contacted a professor of mathematics from the University of Edinburgh, Colin Maclaurin. The three of them collected data on the ages at which people died and used these to calculate how many ministers were likely to pass away in any given year.

Their work was founded on several recent breakthroughs in the fields of statistics and probability. One of these was Jacob Bernoulli’s Law of Large Numbers. Bernoulli had codified the principle that while it might be difficult to predict with certainty a single event, such as the death of a particular person, it was possible to predict with great accuracy the average outcome of many similar events. That is, while Maclaurin could not use maths to predict whether Webster and Wallace would die next year, he could, given enough data, tell Webster and Wallace how many Presbyterian ministers in Scotland would almost certainly die next year. Fortunately, they had ready-made data that they could use. Actuary tables published fifty years previously by Edmond Halley proved particularly useful. Halley had analysed records of 1,238 births and 1,174 deaths that he obtained from the city of Breslau, Germany. Halley’s tables made it possible to see that, for example, a twenty-year-old person has a 1:100 chance of dying in a given year, but a fifty-year-old person has a 1:39 chance.

Processing these numbers, Webster and Wallace concluded that, on average, there would be 930 living Scottish Presbyterian ministers at any given moment, and an average of twenty-seven ministers would die each year, eighteen of whom would be survived by widows. Five of those who did not leave widows would leave orphaned children, and two of those survived by widows would also be outlived by children from previous marriages who had not yet reached the age of sixteen. They further computed how much time was likely to go by before the widows’ death or remarriage (in both these eventualities, payment of the pension would cease). These figures enabled Webster and Wallace to determine how much money the ministers who joined their fund had to pay in order to provide for their loved ones. By contributing £2 12s. 2d. a year, a minister could guarantee that his widowed wife would receive at least £10 a year – a hefty sum in those days. If he thought that was not enough he could choose to pay in more, up to a level of £6 11s. 3d. a year – which would guarantee his widow the even more handsome sum of £25 a year.

According to their calculations, by the year 1765 the Fund for a Provision for the Widows and Children of the Ministers of the Church of Scotland would have capital totalling £58,348. Their calculations proved amazingly accurate. When that year arrived, the fund’s capital stood at £58,347 – just £1 less than the prediction! This was even better than the prophecies of Habakkuk, Jeremiah or St John. Today, Webster and Wallace’s fund, known simply as Scottish Widows, is one of the largest pension and insurance companies in the world. With assets worth £100 billion, it insures not only Scottish widows, but anyone willing to buy its policies.⁷

Probability calculations such as those used by the two Scottish ministers became the foundation not merely of actuarial science, which is central to the pension and insurance business, but also of the science of demography (founded by another clergyman, the Anglican Robert Malthus). Demography in its turn was the cornerstone on which Charles Darwin (who almost became an Anglican pastor) built his theory of evolution. While there are no equations that predict what kind of organism will evolve under a specific set of conditions, geneticists use probability calculations to compute the likelihood that a particular mutation will spread in a given population. Similar probabilistic models have become central to economics, sociology, psychology, political science and the other social and natural sciences. Even physics eventually supplemented Newton’s classical equations with the probability clouds of quantum mechanics.

We need merely look at the history of education to realise how far this process has taken us. Throughout most of history, mathematics was an esoteric field that even educated people rarely studied seriously. In medieval Europe, logic, grammar and rhetoric formed the educational core, while the teaching of mathematics seldom went beyond simple arithmetic and geometry. Nobody studied statistics. The undisputed monarch of all sciences was theology.

Today few students study rhetoric; logic is restricted to philosophy departments, and theology to seminaries. But more and more students are motivated – or forced – to study mathematics. There is an irresistible drift towards the exact sciences – defined as ‘exact’ by their use of mathematical tools. Even fields of study that were traditionally part of the humanities, such as the study of human language (linguistics) and the human psyche (psychology), rely increasingly on mathematics and seek to present themselves as exact sciences. Statistics courses are now part of the basic requirements not just in physics and biology, but also in psychology, sociology, economics and political science.

In the course catalogue of the psychology department at my own university, the first required course in the curriculum is ‘Introduction to Statistics and Methodology in Psychological Research’. Second-year psychology students must take ‘Statistical Methods in Psychological Research’. Confucius, Buddha, Jesus and Muhammad would have been bewildered if you told them that in order to understand the human mind and cure its illnesses you must first study statistics.