CHAPTER 3
The eighteenth-century poet and philosopher Samuel Johnson began his epic poem “The Vanity of Human Wishes” with these lines:
Let Observation with extensive view,
Survey humankind, from China to Peru.
(Johnson, “The Vanity of Human Wishes,” stanza 1)
For our inquiry into how we came to a quantitative Weltanschauung (worldview), Dr. Johnson’s words are more than poetic—they are instructive. The lines carry for us the thought that observation is key to making informed statements and conclusions. Observation forms the basis for systematic inference, the core of much scientific inquiry. In addition, observation can be applied to nearly anything. It has, says Dr. Johnson, “extensive view … from China to Peru,” metaphorically proclaiming its universality of purpose. Further, one can employ such observational purpose intentionally and for a sustained period. Observation here is active, thoughtful, and deliberate, not casual. Accordingly, we learn to apply observation as logical inquiry.
Observation begins our story of the evolution of humankind’s worldview from one of a qualitative perspective to one of quantification.
Common observing—an automatic, ordinary part of daily existence—broadened in scope to become observation—an empirical tool for scientific inquiry. Observation was, at this time, recognized by the greatest of scientists as a pragmatic part of their work, and it gave impetus to a sudden and immense advance in mathematics, one that sharply focused on the invention of methods to calculate uncertainty as a predictable event. In other words, gauging the odds and likelihood of an event is now an evaluable problem with an empirical solution—and significantly, it all began with observation.
What sets these new methods apart from earlier forecasts and predictions was that they were based in mathematics, have estimable accuracy, and are reliable. Over time, the methods of these sciences have become ever more accurate and reliable.
Dr. Johnson seems to anticipate this operational use of observation when he instructs his readers to use observation for a particular purpose: namely, to “survey humankind.” In doing so he invites scientific inquiry. Observation is now methodology. In this context, observation is both affective, as in Dr. Johnson’s poem, and effective when used in scientific inquiry. G. K. Chesterton, the influential nineteenth-century journalist and social critic, called himself “an observationalist.” He bridged the two disparate ways of engaging the world by saying, “The difference between the poet and the mathematician is that the poet tries to get his head into the heavens while the mathematician tries to get the heavens into his head” (Chesterton 1994).
Early astronomers, including Ptolemy, Aristotle, Copernicus, and Galileo, realized the importance of observing phenomena accurately. From the start, they took seriously the role of observation in their studies. Galileo, in particular, had profound insight regarding observation, being one of the first to appreciate variations between his measurements. He systematically studied such differences, attributing them to his varied observations. To account for this, Galileo (and these other early scientists) typically used the “best” observation: that is, the values they employed in their work were from the single observational occasion that was least influenced by immediate distractions or irrelevancies. If, say, an astronomer was observing the relationship between the moon and a given star, he might use in his calculations the numbers gathered on the clearest night.
But, after a while, Galileo and other astronomers switched from their best observation to using the average of their repeated observations. Now, they considered this average value to be the most representative value. Hence, the arithmetic mean of repeated observations became the number customarily employed in their calculations. The difference between the mean and any actually observed value was considered an error in measurement. And, thus, the term “error” came into use in their professional lexicon.
But a contemporary of Dr. Johnson, the German astronomer Tobias Mayer, realized that the arithmetic mean itself may not be the most accurate value to represent a phenomenon, because changes in the conditions under which the measurements are taken are not uniform across all observational occasions. Even slight or subtle variations in the conditions of measurement, multiplied over repeated observations, can grow to be a substantial influence on the outcome. Because of this, the mean is often skewed and therefore can be an inaccurate representation of the phenomenon’s true value. Further, when the phenomenon is itself dynamic, such as the changing orbits of stars and planets, using the mean value is yet more problematic.
From this insight, Mayer suggested an operational method for gathering data useful to scientific inquiry, in a process he called a “combination of observations.” Methodologically, combining observations is different from measurement gathered with repeating observations. Essentially, he sought to reduce the error by systematically controlling the conditions under which the several independent observations were taken, and then combining the information to form a more meaningful value. At first blush, this may seem like a distinction without a difference from merely taking the average, but it turns out to be a significant methodological advance in how data is gathered for scientific analyses.
Mayer devised his imaginative approach to controlling the conditions while studying lunar variation in an attempt to accurately figure longitude. It was reasoned by astronomers that the moon’s position relative to Earth would be an effective way to do this, but the problem for Mayer (and others who also studied the problem) was that the moon’s position relative to Earth is not fixed. It oscillates slightly in a phenomenon known to astronomers as libration. Due to libration, the amount of the moon’s surface visible from Earth varies, to an average of about sixty percent over time. Three types of libration—technically termed diurnal, latitudinal, and longitudinal—were known to exist. When working on the longitude problem, contemporary astronomers would follow the usual practice of taking only three measurements, one for each type of libration but irrespective of its variation.
Mayer took measurements at different hours—three, six, and nine hours apart—to account for variance in libration. For each type of libration, he took three measurements in each period, for a total of twenty-seven observations. He cross tabulated these observations for successive days to identifiable stars, like the sun and Antares (the brightest star in the constellation of Scorpius). Finally, he combined these separate values to produce the representative numbers for his design.
This approach was clever in accounting for variation in libration with multiple measurements within each one of them, and in combining values. His approach is so sensible that to us it may seem unremarkable: simply making his observations at prescribed times during each libration. As one historian of this period noted, “[Mayer’s] approach was a simple and straightforward one, so simple and straightforward that a twentieth-century reader might arrive at the very mistaken opinion that the procedure was not remarkable at all” (Stigler 1986, 21). But, as we understand now, it was a breakthrough in scientific methodology.
From his data, Mayer began solving the longitudinal problem by using methods of trigonometry newly devised by Leonhard Euler (an important Swiss mathematician of the eighteenth century). But, in yet another complication, Euler’s trigonometry could not accommodate Mayer’s many combinations. The difficulty was that he had twenty-seven equations with three unknowns to solve: the diurnal, latitudinal, and longitudinal coordinates.
Not to be stopped at this point, Mayer then worked to advance Euler’s trigonometry so as to handle the increased complexity. While hardly easy math, the longitude problem was nevertheless now one with a solution. Once he had made his calculations, Mayer published longitude tables which were later proved to be accurate within half a degree. (Later still, more precise clocks gave route to determining exact longitudes.) Figure 3.1 shows Meyer’s actual tabulations.
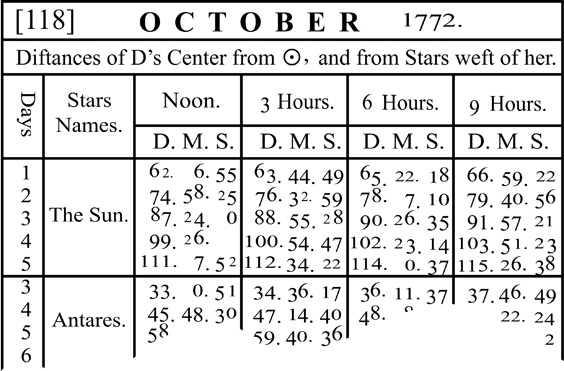
Figure 3.1 Tobias Mayer’s lunar-distance tables
(Source: from T. Mayer, The Nautical Almanac and Astronomical Ephemeris for the Year 1772)
But Mayer’s approach was still a flawed methodology. Its shortcomings were not fully addressed until nearly a century later by Carl Gauss with his method of least squares, which is the approach to synthesizing observational data that we use today. Both Mayer and Gauss lived and worked at the same time as our Dr. Johnson, and while we have no record of their meeting, we can presume that they at least knew of one another because separately they were luminaries of the day. In Chapter 7, I explain Gauss’s monumental accomplishment. As we will see there, too, the invention of the method of least squares was not solely due to Gauss.
Despite Mayer’s ingenuity, his measurement strategy was not readily accepted by his contemporaries. Euler expressly rejected any advantage to Mayer’s system for making observations over the traditional practice of taking the simple arithmetic mean of repeated observations.
Because of Euler’s superior stature among astronomers of the day, most of them followed him and Mayer’s clever approach to observation languished as an undiscovered treasure. But, by the late eighteenth century, Gauss had invented his method of least squares, complete with incontestable math proofs and careful documentation, and that technique finally prevailed. Now, we view Gauss’s method of least squares as a touchstone by which other procedures for synthesizing observational data are judged.
* * * * * *
Euler himself made many important contributions to early mathematics. He followed Newton with some advances in calculus and number theory. But another of his contributions is the one that we see more widely today: his codification of modern mathematical terminology and its notation, like f(x). Most famously, he specified the “order of operations,” which shows which step in solving a mathematics problem should be first, and then what is next. You probably recognize this mnemonic: “Please Excuse My Dear Aunt Sally,” or PEMDAS, for Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. And the practice of working problems from left to right is also thanks to Euler.
Because of these numeric stipulations, he is responsible for our consistency in solving equations like this one:
![]()
You may have, at some point, asked your friends to solve such simple equations just to see how many answers they have. It’s a fun game. Often (sometimes depending upon the number of beers consumed or the lateness of the hour), many different answers are produced. Fifty-five is the correct answer by modern order of operations. Think—and thank—Euler, because it is just practical that we all solve equations in a uniform order.
These contributions—and others—place Euler near the top of all the early mathematicians and make him a harbinger of quantification. Pierre-Simon Laplace (whom we encounter in Chapter 4) articulated Euler’s influence on mathematics by declaring, “Read Euler, read Euler, he is the master of us all.”
Now, without digressing into an account of the history of mathematics (despite it being a great story, too—recall that, in the concluding paragraph of Chapter 1, I cite several works that do tell that story), I pause to acknowledge the work of another noteworthy individual who was also antecedent to our focus on quantification: Gottfried Leibniz. Initially working without an awareness of Newton’s development of calculus, Leibniz would come to his own parallel invention of both differential and integral calculus, although about ten years later. And, in 1679, Leibniz introduced binary arithmetic, which—as many readers will recognize—is the elemental mathematics for directing electronic pathways in microchips.
Aside from astronomy and geodesy, there are many other fields where observation has played an inventive role in scientific inquiry. For example, Charles Darwin, working roughly a century after Dr. Johnson and well within our time frame, based his entire body of evidence for an evolutionary trail in lower animals (and then the human species) on the observations he made of animals and their habitats. His books On the Origin of Species and The Descent of Man, were accepted immediately as revolutionary. He was active, thoughtful, and deliberate in his observations, but he did not include any mathematics to support his description of species evolution, nor was he particularly careful in following research protocols, despite their being well established by his time. We explore more about Darwin and his influence on quantification in Chapter 12.
Today, we label the methodology used by Darwin as “observational research,” or sometimes more narrowly as “naturalistic inquiry.” Observational research is nonexperimental study wherein the researcher systematically observes ongoing behavior, while the term “naturalistic inquiry” typically suggests that the research is field based, as opposed to being conducted under controlled, experimental conditions.
* * * * * *
Stemming from observation as the opening to our story of quantification, it is necessary to mention two other forerunners to the principles in our story, if only briefly. They are Sir Isaac Newton (in England) and Blaise Pascal (in France). Both men directly influenced almost all the individuals we meet in this book. Almost certainly, readers will recognize the names of these giants of early scholarship. Each made monumental achievements in mathematics, astronomy, physics, philosophy, and elsewhere. I introduce Newton in this section and Pascal in the next. Both Newton and Pascal slightly precede the timeline of our story of quantification; nonetheless, each is so consequential to the persons and events we do address that they deserve some note.
Newton, in particular, is widely credited (with agreement from Einstein) as perhaps the most influential scientist of all time. He virtually invented the physics of motion and gravitation, formulated modern calculus, and procedurally set out the scientific method. Of course, there were earlier attempts to mathematically describe motion and force (the essential focus of calculus), but Newton provided direction and solvable equations for these ideas, thereby giving a structure to modern mathematics. And, with his advanced description of the laws of gravity, he presages Einstein’s theory of relativity.
The lasting impact of this brilliant individual on our lives cannot be overstated—we will see his influence throughout the story of quantification. His thinking dominated scientific inquiry for more than three centuries.
He was truly one of a kind. An early Newton scholar and translator of his work (from Latin into English) describes the man in almost reverential tones: “the author, learned with the very elements of science, is revered at every hearth-stone where knowledge and virtue are of chief esteem” (Newton, Motte, and Chittenden 1846, v). Further, Newton was the first person appointed to the position of Lucasian Professor of Mathematics at Cambridge University, probably the most prestigious appointment in all academia. He held the chair from 1669 to 1702. It has been occupied by luminaries ever since; for example, it was held by Stephen Hawking from 1979 to 2009. The position is popularly referred to as “Newton’s chair.” Newton was widely renowned during his lifetime; his fame then was parallel to that of Einstein in the early twentieth century. Among innumerable tributes to Newton work and life is the honor of having an elite private school and a fine college named after his masterwork, Principia.
Upon Newton’s death in 1726, the poet Alexander Pope wrote the following epitaph:
NATURE and Nature’s laws lay hid in Night:
God said, Let NEWTON be! and all was Light!
(Pope, “Epitaph: Intended for Sir Isaac Newton”)
I wholeheartedly suggest reading something about Newton’s life and accomplishments, since he continues to be important in our lives today—but chiefly because doing so places one in the company of a truly remarkable man. A fine list of books is available online, provided by the Isaac Newton Institute for Mathematical Sciences in Cambridge (see Isaac Newton Institute for Mathematical Sciences 2018).
Another honor given to Newton is the life-size statue of him at Trinity College, Cambridge University. This statute, by Louis-François Roubiliac, was presented to the college in 1755 and has been described as “ the finest work of art in the College, as well as the most moving and significant” (Oates 1986, 204). It is inscribed with Qui genus humanum ingenio superavit (“Who surpassed the race of men in understanding”). It is shown in Figure 3.2.

Figure 3.2 Statue of Isaac Newton at Trinity College, Cambridge
(Source: http://commons.wikimedia.org/wiki/Category:Public_domain)
Newton left us with many memorable quotes. A few of his best-known ones are the following:
If I have seen further it is by standing on the shoulders of Giants. (Newton, Isaac. (1675) 2017)
To explain all nature is too difficult a task for any one man or even for any one age. Tis much better to do a little with certainty & leave the rest for others that come after you [than] to explain all things by conjecture without making sure of any thing. (The Newton Project. 2011)
To every action there is always opposed an equal reaction: or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts. (Newton, Motte, and Chittenden 1846, 83)
Gravity explains the motions of the planets but it cannot explain who sets the planets in motion. (The Newton Project, 2011)
About the same time as systematic observation was beginning to be recognized as an essential tool of science (that is, in Dr. Johnson’s time), the Principia was translated from Latin into English, an act that ensured its broad influence. Almost every scholarly work on a quantitative subject has its genesis in Newton’s momentous work. It forms the foundation for entire fields of higher mathematics and philosophy. From its initial publication in 1687 to today (a time span more than three centuries long), Newton’s Principia has been considered to be an example of science at its best.
Several copies of the first edition of the Principia survive. Newton’s own copy with his handwritten notes is located at Cambridge University Library, and another copy is at the Huntington Library in San Marino, California. One copy, which was originally a gift to King James II, sold in 2013 at auction for nearly three million dollars. Its title page is shown in Figure 3.3.

Figure 3.3 The title page from Isaac Newton’s Philosophiæ Naturalis Principia Mathematica
(Source: http://commons.wikimedia.org/wiki/Category:Public_domain)
As for Principia’s content, Newton’s work is a touchstone for modern mathematics and physics. Only a generation before, mathematics had been an immature field of inquiry mostly confined to straightforward measurements in astronomy and geodesy. Its emphasis was upon using early geometry and trigonometry to learn more about characteristics of celestial bodies, like their size and distance from where mere mortals stood. There was no developed investigation into predicting their orbits or learning why some planets move faster than others. At the time, most persons, including astronomers, did not envision such questions. The predominant thinking was that everything in existence was controlled directly by God. (Virtually everyone at the time held strong religious beliefs.) The stars and planets had orbits known only to “Him” and controlled exclusively by “Him.” It was imagined that nature was at the whim of God.
This was a time much prior (by about one hundred years or so) to the era of our story: quantification as a worldview was something no one dreamed of.
Then Newton came along. He was the first person to truly realize how things in nature behave and why it is so. He turned the world upside down by realizing and understanding the physics of the cosmos. Building upon Copernicus’s work, Newton discovered that there are physical laws that operate across the universe, beyond just here on Earth. The most universal and consequential physical law is that of motion: specifically, gravity. Newton discovered gravity and the laws of gravitation, as specified in the three laws of motion.
He saw that gravity makes an apple fall and that it also is the reason why an object’s trajectory is eventually drawn downward. If you throw a rock, for instance, it travels forward only for a bit before its trajectory begins to bend downward, owing to the silent force of gravity. With astounding insight, Newton realized, too, that gravity operates outside of the Earth and that it explains the orbits of celestial bodies. He saw, even, that the moon is held in place by gravity. As we know now, with calculable precision, that if a spaceship travels at the same speed as Earth’s rotation, its trajectory will bend downward in correspondence to Earth’s curvature. This is exactly how the International Space Station is kept in orbit today.
Newton not only made his observations as philosophical argument, he provided a mathematical scheme to define gravity—modern calculus. And, as readers likely know, calculus forms the underpinning for nearly all of modern mathematics, including probability theory, as we study in this book. It is simply amazing. Newton set the groundwork for all of quantification.
* * * * * *
While mentioning Newton as the developer of modern calculus, I also want to reassure you about references herein to this higher form of mathematics. Throughout our story, I necessarily cite calculus as a field in mathematics; however, I will remain true to my pledge in Chapter 1 to not use any calculus to solve equations. In this book, we will not “solve” any equations, as that is not our focus. I only mention the term calculus (or algebra or geometry) to let you know where the mathematics lie. We will encounter the word often throughout this book. Just read the word calculus as our story unfolds—you will not be lost.
Still, a short explanation of calculus may be interesting because it is so foundational to probability theory. To grasp a very primary notion of calculus, realize that it is as much a way of thinking as a system for devising and solving equations that follow a set of mathematical principles. Calculus is a method of mathematically addressing questions about quantities that change, particularly when the change is nonlinear. Typically, in science, change is classified into two branches: rate of change (called “differential calculus”), and accumulation or change up to a certain point (called “integral calculus”). Thus, calculus itself has two complementary branches: differential calculus and integral calculus.
In both instances, the measurement is done by estimating the change many, many times, essentially breaking the measurement down into small pieces and then measuring each bit and incrementally summing them to get the useful, big picture. Knowing this, we can appreciate logically that the word calculus itself derives from the Latin, meaning “small stones,” because it is a way to understand something by looking at its small pieces.
We can see these calculus estimates for change through an example. Consider the speed of a bullet. There is an exit velocity for a bullet as it leaves a gun barrel. The velocity soon changes due to many factors, such as air resistance, loss of inertia, and, most forcefully of all, gravity. Hence, a bullet does not move in a straight line forever; rather, its trajectory is an arc, and its rate of change continually slows, just like the rock and the spaceship. With calculus, you can compute the force or energy (e.g., rate of change, or speed) at any point along the arc.
Integral calculus can be illustrated by imagining a bell-shaped curve, the kind with which we are so familiar (actually, any shape of a curve, but this is the shape with which we are most accustomed). Now, see below the curve a straight horizontal line, the baseline. Visualize some point along the baseline—say, the midpoint. Then, take a second point some distance above it, to its right side. Project for both points a straight vertical line extending upward to the curve, thus graphically specifying a portion under the curve as between these lines. With calculus, we can determine the area under the curve that we have specified. In fact, in educational and psychological testing, this area under the bell-shaped curve represents percentiles of the tested population (in this example, since we are starting at the midpoint, it is the percent above the fiftieth percentile). In Chapters 9 and 14, I discuss this point in a more complete context (for an illustration for our current discussion, see Chapter 9, Figure 9.5).
Relatedly, by using the inverse of what I just described, calculus can be employed to determine the volume of any shape, even when it is an irregular shape. Here, think of some three-dimensional shape, like a sphere, a capsule, a cone, a pyramid, or even something less regular in its shape, such as an amoeba. Calculus, with integration, can estimate the volume of these shapes.
This is as technical as I go in this book. Obviously, I am leaving out many important and fascinating features of calculus, but, as Father William in Lewis Carroll’s poem of the same name said:
“I have answered three questions, and that is enough,”
Said his father. “Don’t give yourself airs!
Do you think I can listen all day to such stuff?
Be off, or I’ll kick you down-stairs!”
(Carroll, “Father William,” stanza 8)
Still, beyond just explaining the essential core of calculus, it is instructive to realize its many uses. As one can imagine, calculus is so broadly applicable it is difficult to think of areas of work where it is not useful. For instance, in construction, it is vital in estimating the strength of materials for a bridge spanning a gorge; in addition, calculus is used to determine the rate at which the concrete of the bridge degrades. In medicine, calculus helps medical researchers determine appropriate drug dosages, again by estimating the rate of change. And, of course, it is employed with missiles and rockets for everything from optimizing their materials during construction to setting their trajectories. In biology, it is helpful in determining the effects of environmental factors on a species’ survival. In finance, it can be used to identify which stocks would compose the most profitable portfolio. As we just saw, in educational and psychological testing, calculus is used to figure percentiles. In manufacturing, calculus aids in reckoning optimal industrial control systems … and on and on.
One of the most imagined examples for calculus is its application in determining the path of a celestial body such as a star, planet, or asteroid. Like the trajectory of a bullet, a celestial body does not travel in a straight line through infinite space. It, too, is pulled downward by the gravity of whatever object (e.g., the sun or Earth) is close enough to exert influence. Thus, as Earthlings, we orbit the sun; and similarly, the moon’s orbit is fixed by Earth’s gravity. This is so for all celestial objects in our solar system, and in others. Because not everything is exactly regular (e.g., Earth is not a perfect sphere, and it does not spin at a uniform rate), an orbital path is an ellipsoid. When a rocket’s falling trajectory exactly matches Earth’s rotation, the rocket remains in Earth’s orbit. Astronauts could (theoretically, at least) orbit Earth forever; but fortunately, they can break the force by turning on thrusters to head back home.
At this point in our discussion of observation, some readers may think of the field of statistics, as it too relies on numerical quantities gathered from observations that change. But this term was not used until later, around the mid-eighteenth century, when Gottfried Achenwall was systematically gathering numbers for his employer (the German government) and called his system “statistics” (the original German is Statistik or “political state”). Some historians claim that, owing to his development of these structured methods, Achenwall is the “father of statistics,” although others challenge that ascription, claiming it really belongs to Sir Ronald Fisher who, much later, virtually invented modern statistics by introducing inferential reasoning to hypothesis testing and many other methodologies. (We meet him in Chapter 14.) Achenwall, however, appears to have been the first one to use the name “statistics” to describe his organizing work.
* * * * * *
The other earlier giant in mathematics who influences so many of the individuals in the story of quantification is Pascal. In truth, our story of quantification could logically begin with him, since he was instrumental in the founding of probability theory as a distinct discipline. We will see his work and influence many times in this book.
Pascal was a man of truly extraordinary intellect, and stories of his mathematical exhibitions when he was still a child abound. For one, while in elementary school, he almost fully memorized Euclid’s elemental geometry treatise Elements of Geometry. Also, it is reported that when his teachers gave him a problem in mathematics, he often accompanied his answer with a proof. One imagines his schoolmates were not similarly occupied!
To help with his father’s business as a local tax collector, Pascal invented a simple wooden calculating machine that he called the “Pascaline,” or the “Arithmetic Machine.” It is probably the first machine produced in any quantity to actually perform arithmetic operations. It calculated by rotating wheels of numbers which could be added and subtracted. He later made attempts to have it do multiplication but was not successful. His original Pascaline is on display at the Musée des Arts et Métiers in Paris and is shown in Figure 3.4. It has been reproduced by hand many times, in brass, in silver, and in wood. And his machine predates Leibniz’s “Stepped Reckoner,” which some consider to be the first calculator because it could perform all four arithmetic functions.

Figure 3.4 Pascal’s Pascaline
(Source: http://commons.wikimedia.org/wiki/Category:Public_domain)
One of Pascal’s most consequential achievements was not a physical contraption at all. Rather, it was his conception of a simple graphic triangle that displays solutions to some common expansions of the binomial. The binomial theorem is foundational to probability theory, as well as to much of algebra—indeed, to all of number theory. And “Pascal’s triangle” is a clever arrangement of numbers that makes solving some of the binomial’s numerical expansions quick and easy. In Chapter 4, we meet both of these numerical inventions: the binomial theorem and Pascal’s triangle.
Early on, Pascal turned his attention to studying probability, which, at the time, was not an organized field of academic scholarship but more just an interest of persons concerned about getting ahead in their gambling bets. Pascal’s interest began when he learned of a special gaming scenario now called “the unfinished game,” but which, for a long time, was known as the “problem of points.”
The problem of points presents a simple illustration of chance, or, more to our perspective, the notion of how to measure uncertainty. In the “game,” two players contribute equally to a pot of money. They then agree to an upper limit of trials for some chance event (like the rolling of a die, or the flip of a coin), at say, ten trials each, after which whoever leads takes the entire pot. This is simple enough; the “problem” comes into play when, hypothetically, the game is interrupted before it is finished.
The question for the players is how to divide the pot for an incomplete game. Obviously, it would be unfair to give the winnings to the leader midway through, since the loser would not have had an opportunity to switch places to be the winner himself. Or, one might suggest that the pot be divided proportionally according to how many points were won up to the time when the game stopped, a solution proposed by Luca Pacioli, an early mathematician who studied the problem and who worked with Leonardo da Vinci on a fascinating book on mathematics and art, De Devina Proportione (On the Divine Proportion). (We will explore this book in Chapter 17.)
But that proportional solution was thought to be unsatisfactory by two other early mathematicians, Gerolamo Cardano and Niccolò Tartaglia. They noted that if the interruption came after only one player had a single trial, it would be far too early in the game to have that division of the pot of money be fair. Over the following years, others, including even Galileo, attempted to solve the problem but also without success. The intractable problem gained attention among mathematicians (and, presumably, gamblers), in large part because it was germane to their interests but seemingly unsolvable.
Finally, in the mid-seventeenth century, Pascal stepped in to work on the problem of points. He was enlisted to tackle it by his friend Antoine Gombaud, Chevalier de Méré, who thought the mental activity would be helpful to the bright-but-frail Pascal as a way to divert his attention away from his poor health, on which he seemed fixated. Pascal agreed to take on the challenge, but he wanted some help. The Chevalier de Méré suggested an acquaintance, Pierre de Fermat. Pascal wrote Fermat a letter to inquire of his interest in joining him in seeking a satisfactory solution to the problem of points. Fermat immediately accepted the invitation, and thus began their famous correspondence. (They never met personally.)
Their five letters discussed the problem of points as a science, the first time it was so described. With immediate insight, they appreciated that the problem was one of estimating the likelihood of a given final outcome from however many points had been won up to the interruption. They each had a different approach, but together they developed a method to calculate risk, the likelihood of success or failure. As consequence, their work formed the foundations of probability theory.
The Pascal–Fermat correspondence is credited with being the first serious study of probability. Due to popular reception of their correspondence, Pascal and Fermat are jointly cited as the “fathers of probability.” Their original correspondence survives and can be viewed online (see original correspondence at Fermat and Pascal 1654). It is charming reading. Moreover, the tale is fully told in a recent book whose title trumpets the significance of their correspondence: The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern (Devlin 2008). While the correspondence is significant, this retelling seems to go a bit further in interpreting its impact on probability than we see in the case of quantification at this time.
Pascal was a man of deep religious conviction, and he revolved much of his thinking about probability around religion. As one example of his linking probability to religion, he argued that a deep-seated belief in God is worthwhile for even the skeptic because, just with the slightest probability of God’s existence, it is better to be with God after death than without. This proposition is famously known as “Pascal’s wager.” Pascal detailed his religious musings at great length in his famous Christian apologetic Pensées, which was unfinished at the time of his death in 1662 but published posthumously in parts over the next several years. Physically, he was unwell most of his adult life and died at age thirty-nine, probably of a stomach tumor.
In the same year as the Pascal–Fermat correspondence took place, the Dutch mathematician Christiaan Huygens published a small manual on probability: De Ratiociniis in Ludo Aleae (On Reasoning in Games and Chance), now considered to be the first published work on probability (Andriesse 2005). However, possibly even earlier, the Italian Renaissance mathematician Gerolamo Cardano (the same person who helpfully dismissed the proportional solution in the “point’s problem”) addressed the probability of given outcomes in rolls of dice, in a paper that has since been lost.
And work on the chances of expecting certain rates of birth and death was done by an obscure London shopkeeper named John Graunt, who taught himself calculus (quite extraordinary for then—and today). He published his investigations in a paper and was later admitted to the prestigious French Academy of Sciences. One imagines that Graunt went into the wrong line of work!
For the most part, the early scholars of probability focused their work on increasing the odds of winning in games of chance; only incidentally did they address measurement error, an essential interest in modern probability theory. Still, these efforts evidence the start of probability theory as a distinct discipline, albeit quite undeveloped at this early stage. From these labors, we can anticipate that measurement science had a bright and burgeoning future, and, alongside it, observation was finding a home. Thus, combining Mayer’s idea of linearly associating observations with the early probability investigations of Pascal, Fermat, and others gave seed to a promising science.
Significantly, from its inception as a discipline, probability theory has been thought of as having practical implication. With it, problems in society, such as anticipating rates for births and deaths or calculating military probabilities in war scenarios, as well as the age-old wish to decrease uncertainty in games of chance, can be approached as having an empirical solution.
To no one’s surprise, at the time, work in probability theory remained in the purview of scholars and academics, who were based primarily at universities, although a few of them were in religious orders and even fewer worked in government. Meanwhile, the vast majority of people—the populace at large—went about their daily lives, unaware of and unconcerned about these mathematical attainments. Quantification had not touched their lives in impactful ways and certainly did not constitute their worldview. The choices they made, both big and small, were done with the immediacy of their thoughts and by their personal experience. It is possible they may have discussed choices with friends or relatives and asked for advice or shared personal experiences. But empirical examination of daily phenomena was not yet anywhere in their mindset.
Thus, the seeds for quantification were being sown but had not yet sprouted.
At that time, even the educational system was limited in its impact on moving people to quantification as a worldview. For students, mathematics likely comprised just the basic four operations of arithmetic (add, subtract, multiply, and divide). Despite the fact that algebra, geometry, and part of trigonometry (along with Newton’s and Pascal’s newly invented calculus) were developed subjects, we know from contemporary accounts that they were not taught in most schools, owing to an insufficient number of qualified teachers and a lack of texts and other resources.
However, this form of higher mathematics was taught in at least a few secondary schools and, of course, in universities. In 1770, Euler published his Algebra, probably the first formal textbook on the subject. And Euclid’s Elements of Geometry was the standard text on geometry from the time it first appeared in 1492 through the mid-eighteenth century.
One historian of the period reports that military textbooks commonly included tables of squares and square roots, something useful for military leaders when preparing orders to deploy troops, and provides this quote from a contemporary military treatise: “Officers, the good ones, now had to wade in the large sea of Algebra and numbers” (Crosby 1998, 6–7).
With “Algebra and numbers” required for military personnel (or at least “the good ones”), calls to mind a scene in Shakespeare’s Othello (fully, The Tragedy of Othello, the Moor of Venice) in which Iago expresses to Roderigo his frustration with his chosen officer Cassio, who was apparently strong in mathematics but lacked practical experience for setting troops in a battlefield (Shakespeare and Rowse 1978). The Bard writes,
I have already chose my officer.
And what was he?
Forsooth, a great arithmetician,
One Michael Cassio, a Florentine,
A fellow almost damn’d in a fair wife;
That never set a squadron in the field.
(Othello, act 1, scene 1)
Othello was written about fifty years before the first probability publication, which tell us numeracy was common even in his time, but certainly not yet part of a broad mindset.